1. 단순 선형 회귀

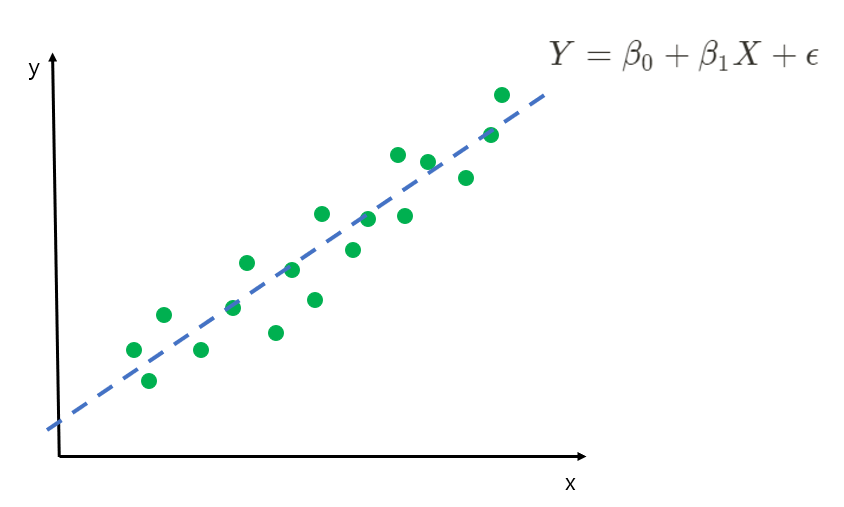
위의 그림에서 초록색 점들은 주어진 데이터이고, 파란색 선은 데이터에 적합한 선인 회귀선으로 볼 수 있습니다. 이때, 단순 선형 회귀식은 ${Y = \beta_0 + \beta_1X + \epsilon}$과 같이 나타낼 수 있습니다.

$\beta_0, \beta_1$는 회귀계수(regression coefficients)이며 데이터로부터 추정해야 하는 값입니다.

$\hat{\beta_0}, \hat{\beta_1}$은 예측된 회귀계수이고, 잔차는 실제값(Y) - 예측값($\hat{Y}$)입니다.

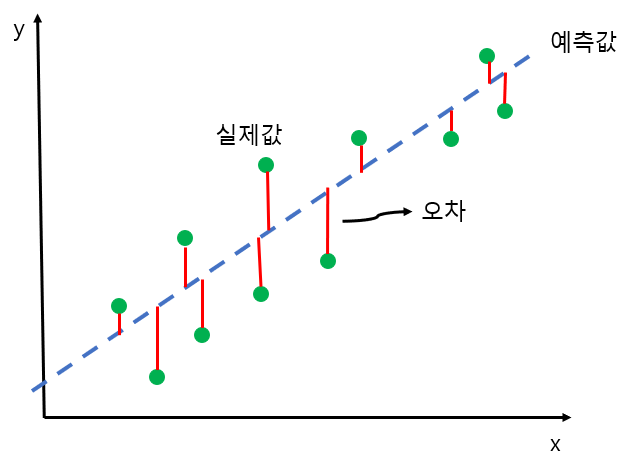
오차는 회귀선 위의 값, 즉 추정된 예측값($\hat{Y}$)과 실제값(Y) 간의 차이를 말합니다.
최적의 회귀 모델은 예측값과 실제값 간의 차이인 잔차 합이 최소가 되는 최소제곱법(OLS) 모델을 이용합니다. 회귀분석은 이러한 오차를 최소화하는 회귀선을 추정해 최적의 회귀계수(모수)를 추정할 수 있습니다. 오류의 합을 구할 때 흔히 사용되는 기법은 잔차제곱합(RSS: Residual Sum of Squares)와 평균절대오차(MAE: Mean Absolute Error)가 있습니다.

우선, 잔차제곱합에 대해 자세히 알아보겠습니다.

${RSS = \sum (y_i - (\beta_0 + \beta_1x_i))^2}$

RSS는 비용이며, 회귀계수로 구성되는 비용함수이자 손실함수라고도 일컫습니다. RSS를 최소화하는 $\beta$ 추정량을 최소제곱 추정량(LSE)라고 합니다.

2. 경사 하강법(Gradient Descent)

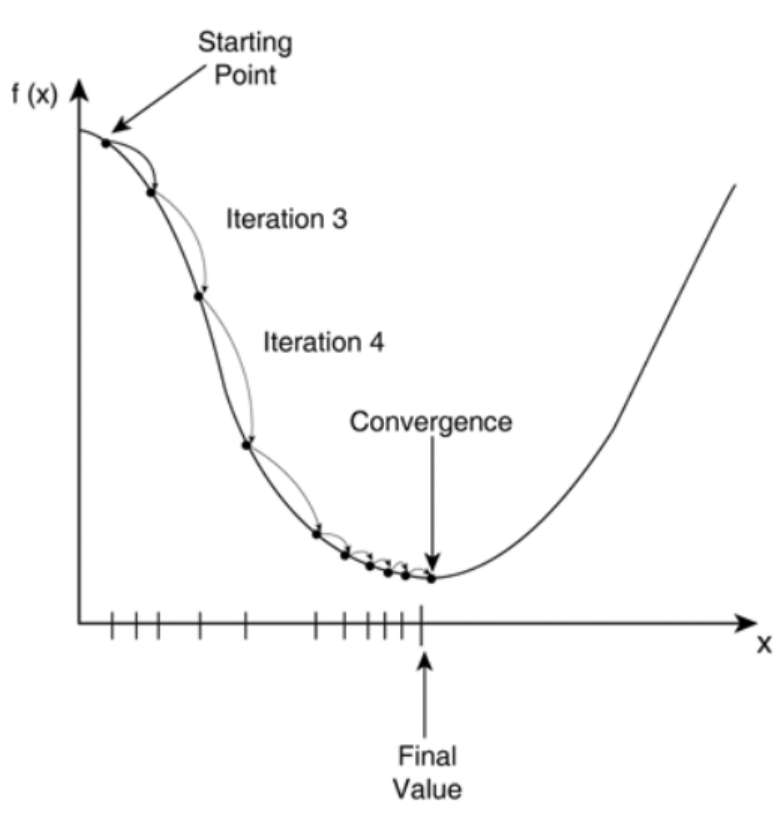
비용함수 RSS를 최소화하기 위해 사용되는 $\beta$ 파라미터를 구하기 위한 방법으로 경사 하강법 을 이용합니다. 경사 하강법은 반복적으로 예측값과 실제 값의 차이가 작아지는 방향성을 가지고 $\beta$ 파라미터를 지속해서 보정해 나가고, 더 이상 오륫값이 작아지지 않으면 최소 비용으로 판단하고 그때의 $\beta$ 값을 최적 파라미터로 반환하는 과정을 거칩니다.

출처

비용 함수가 위의 그림과 같은 2차 함수라면 starting point에서 미분을 적용한 후 미분값이 감소하는 방향으로 파라미터를 업데이트하게 됩니다. 그리고 더 이상 기울기가 감소하지 않는 지점(convergence)을 비용함수가 최소인 지점으로 간주하고 $\beta$ 값을 반환합니다.