1. 회귀 평가 지표

Python statsmodel 패키지의 OLS 클래스로 선형 회귀분석을 실시할 수 있습니다. 모형 선택 기준에는 다양한 방법이 있으며 하나씩 알아보겠습니다.

1-1. MAE

MAE(Mean Absolute Error) 는 실제 값과 예측한 값 차이를 절댓값으로 변환한 후 평균한 것입니다. MAE는 제곱하지 않아 단위가 기존 데이터와 같아 회귀계수의 증감에 따른 오차를 쉽게 파악할 수 있습니다. MAE의 식은 아래와 같습니다.

${MAE = \frac{1}{n}\sum|Y_i - \hat{Y_i}|}$

1-2. MSE

MSE(Mean Squared Error) 는 실제 값과 예측한 값 차이를 제곱해 평균한 것입니다. 잔차의 제곱하는 이유는 음수 값이 됨을 방지하고, 오차의 민감도를 높이기 위함입니다. MSE의 식은 아래와 같습니다.

${MSE = \frac{1}{n}\sum(Y_i - \hat{Y_i})^2}$

1-3. RMSE

RMSE(Root Mean Squared Error) 는 MSE에 루트를 씌운 것입니다. RMSE 식은 아래와 같습니다.

${RMSE = \sqrt{\frac{1}{n}\sum(Y_i - \hat{Y_i})^2}}$

1-4. 결정계수(R-squared) & 조정된 결정계수(Adj.R-squared)

결정계수는 전체 제곱합(SST) 중 회귀식으로 설명할 수 있는 부분(SSR)이기에, 1에 가까울수록 예측 정확도가 높습니다. 조정된 결정계수를 사용하는 이유는 독립변수가 추가되면 SSR이 커지기 때문에 결정계수 값이 무조건 커지는 문제점이 발생하게 됩니다. 따라서 독립 변수의 개수에 대한 페널티를 부과함으로써 조정된 결정계수를 사용하게 됩니다.

1-5. F- statistic

F 통계량은 모형 자체의 유의함을 판단하는 기준입니다. 즉, 모든 독립변수의 계수가 0인지, 하나라도 0이 아닌지를 판별하게 됩니다.

1-6. t- statistic

t 통계량은 독립변수의 유의함을 판단하는 기준입니다. 즉, 해당 독립변수의 계수가 0인지 아닌지를 판별하게 됩니다.

2. 로지스틱 평가 지표

로지스틱 회귀분석은 분류에 가깝기 때문에 파트 2 평가지표에서 설명한 부분은 참고하시면 됩니다.

2-1. Classification Threshold(임계값)

출처

로지스틱 함수로 구한 확률이 cutoff 이상이면 1, cutoff 이하이면 0으로 판단합니다.

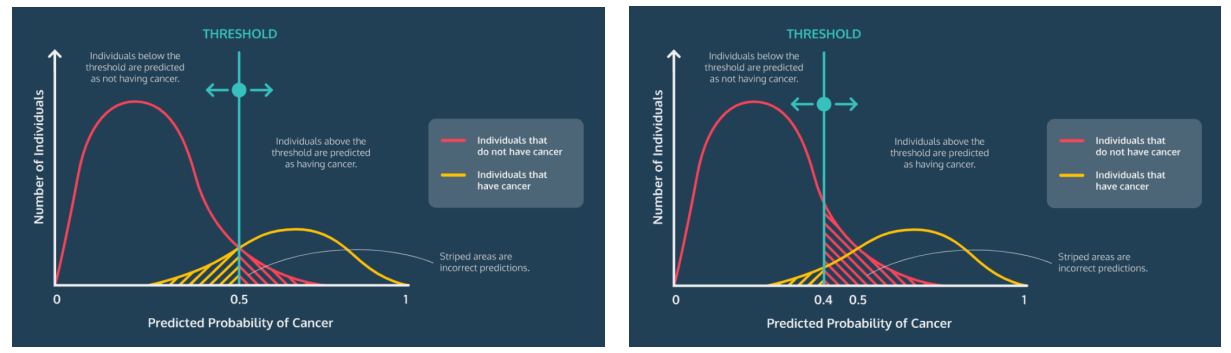
위의 그림에서 빨간색 선은 암이 없는 사람이고, 노란색 선은 암을 가지고 있는 사람입니다. threshold 왼쪽으로 빗금 친 노란색 부분은 암이 있음에도 없다고 예측한 부분이고, threshold 오른쪽으로 빗금 친 빨간색 부분은 암이 없음에도 암이 있다고 예측한 부분입니다. 따라서, 그림에서 빗금 친 부분은 부정확한 예측을 한 경우입니다.

왼쪽 그림은 임계 값을 0.5로 설정했고, 오른쪽 그림은 0.4로 임계 값을 조정했습니다. 조정한 후, 빨간색 빗금 친 영역이 늘어나고 노란색 영역은 줄어들었습니다. 이는 암이 없음에도 암 환자라고 예측한 경우가 늘어나고, 암이 있음에도 없다고 예측한 경우는 줄어든 사례입니다.

이처럼 질환이나 사기 탐지의 경우에는 유병, 사기 케이스에 매우 민감하기 때문에 필요에 따라 Cutoff를 변경해 민감한 부분의 예측 정확도를 높이는 성능 조절이 가능합니다.