회귀진단이란 데이터가 회귀분석에 사용된 모형의 가정을 제대로 만족하고 있는가에 관해 확인하는 과정입니다.

회귀진단에는 총 4개의 회귀모형의 기본 가정이 있습니다.

1. 선형성(Linearity) : 독립변수(X)와 종속변수(Y) 간 선형 관계를 만족하는가
2. 정규성(Normality) : 오차(Error)의 정규성을 만족하는가
3. 등분산성(Homoscedasticity) : 오차의 등분산성을 만족하는가
4. 독립성(Independence) : 오차의 독립성을 만족하는가

1. 선형성(Linearity)

선형성이란 독립변수와 종속변수 간의 선형 관계에 대한 가정입니다.따라서 독립변수와 종속변수 간 산점도(Scatter plot) 를 통해 선형성을 판단하게 됩니다.

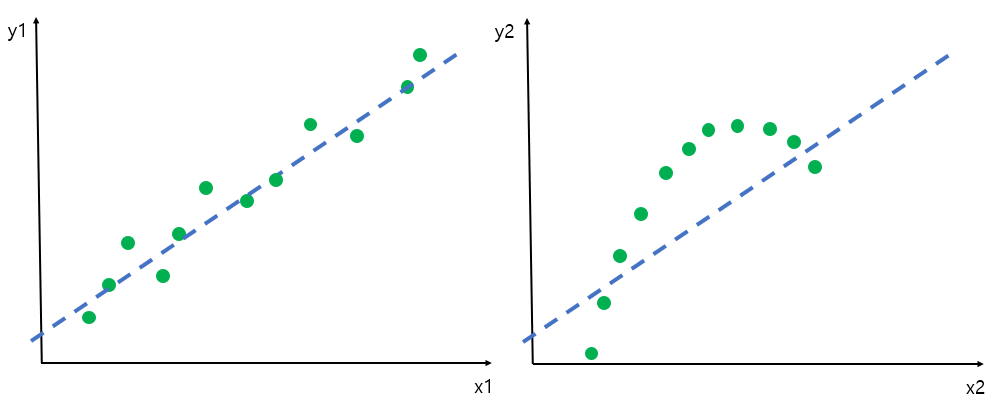
위의 첫 번째 그림은 $x_1$과 $y_1$이 선형 관계라고 볼 수 있지만, 두 번째 그림은 $x_1$과 $y_1$이 선형 관계가 있다고 보기 어렵습니다.

선형성 가정을 만족하지 않을 때는 여러 가지 방법이 있습니다.

1. 다른 새로운 변수를 추가해봅니다.
2. 로그, 지수, 루트 등 변수 변환(Transformation)을 취할 수 있습니다.
3. 선형성을 만족하지 않는 변수를 제거할 수 있습니다.
4. 선형 회귀모델을 생성한 후 변수 선택법을 통해 변수를 통과시키는 방법이 있습니다.

2. 정규성(Normality)

정규성이란 오차가 정규분포를 따라야 한다는 가정입니다. 잔차의 히스토그램을 통해 오차의 정규성을 판단할 수 있습니다.

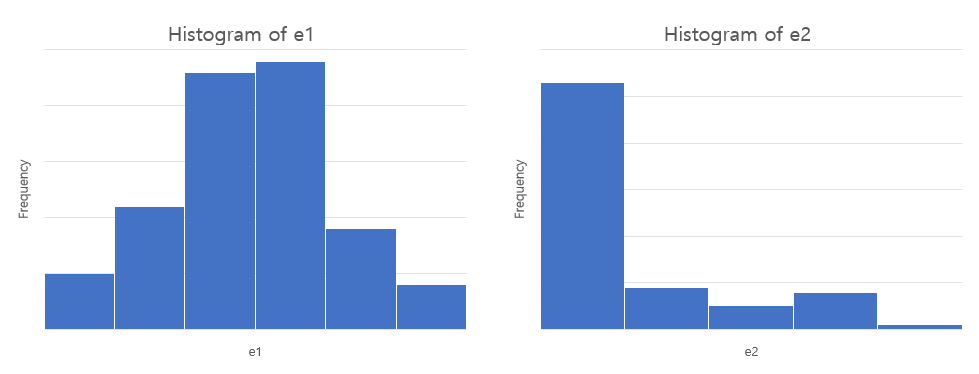
위 그림에서 $e1$은 정규성 가정을 만족하지만, $e2$는 위배한다고 볼 수 있습니다. R에서는 Shapiro-Wilk Normality Test를 통해 판단할 수 있습니다. 정규성 가정이 만족하지 않는 경우, log나 root을 취해서 오차를 정규분포 형태로 취하게 만들 수 있습니다.

3. 등분산성(Homoscedasticity)

등분산이란 분산이 일정한 것이며, 즉 특정한 패턴 없이 고르게 분포한다는 의미입니다. 독립변수에 대한 잔차로 오차의 등분산성을 판단합니다.

왼쪽 그림은 대역폭(band width) 가 일정하지만, 오른쪽 그림은 점점 커지는 이분산이기 때문에 등분산성 가정을 만족하지 않습니다. 등분산성이 만족하지 않는 경우, 변수를 로그 변환한 트랜스로그(translog) 모형을 사용하면 해결되는 경우가 있습니다.

4. 독립성(Independence)

독립성이란 독립변수 간의 상관관계가 없이 독립성을 만족하는 것을 말합니다. 그러므로 단순 회귀분석은 해당하지 않고, 다중 회귀분석의 중요한 가정이 됩니다. 독립변수와의 상관성과 자기 상관성을 확인해 독립성을 판단하게 됩니다. Durbin-Watson 검정과 **ACF(AutoCorrelation Function)**를 통해 독립성을 판단할 수 있습니다.

4-1. Durbin-Watson

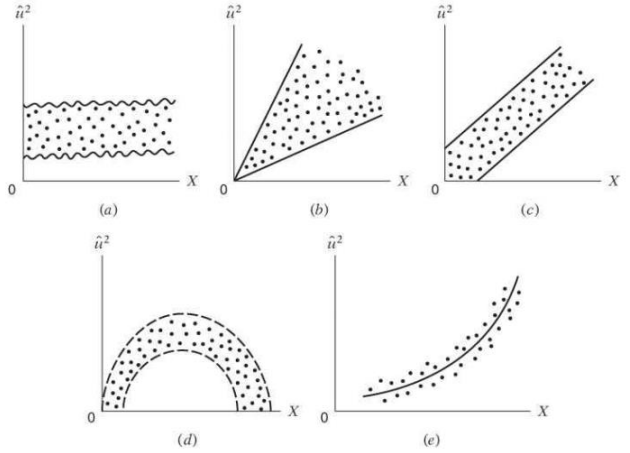
회귀진단에서의 오차의 독립성을 검정하기 위한 방법입니다. 0에서 4 사이의 값을 가지는데, 0에 가까우면 양의 상관관계, 4에 가깝다면 음의 상관관계, 2에 가까우면 독립성을 만족한다고 할 수 있습니다.

출처

위 그림의 경우 (a) 를 제외한 나머지는 패턴을 가지기 때문에 독립성 가정을 위배한다고 볼 수 있습니다. 독립성을 만족하지 않는 경우, 즉 다중공선성(Multicollinearity)이 생긴다면 제거해주어야 합니다.

4-2. 다중공선성(Multicollinearity)

다중공선성 문제는 독립변수 간의 강한 상관관계가 나타나는 현상입니다. 다중공선성은 독립변수의 산점도, heatmap, 상관계수 행렬로 파악이 가능합니다. 다중공선성이 존재하면 회귀계수의 추정이 불안정해지기 때문에, 줄이기 위해 노력해야 합니다. VIF(Variance Influence factor)가 10보다 크면, 다중공선성이 존재한다고 판단합니다. 단, VIF 값이 크더라도 해당 독립변수가 통계적으로 유의한다면 제거하지 않는 것이 바람직하다고 볼 수 있습니다.

다중 공선성을 제거하는 방법에는 크게 2가지 방법이 있습니다.

1. All possible regression : 전진 선택법, 후진 제거법, 단계적 방법
   • 전진 선택법(forward selection) : 상관계수가 높은 순서대로 변수를 추가하는 방법이며, 유의수준 알파를 만족하는 변수가 없는 경우에 변수 선택을 마칩니다. 이때, 추가된 변수는 제거되지 않습니다.
   • 후진 제거법(backward elimination) : 모든 변수를 포함하는 상태에서 유의하지 않는 변수를 제거하는 방법입니다. 이때, 제거된 변수는 다시 추가되지 않습니다.
   • 단계적 방법(stepwise method) : 전진 선택법과 후진 제거법의 혼합형태로서, 변수를 선택한 다음 선택된 변수 중에서 제거할 변수가 있는지 확인합니다. 이때, 추가된 변수는 제거할 수고, 제거된 변수를 다시 추가할 수도 있습니다.
2. Embedded : 릿지(Ridge), 라쏘(Lasso), 엘라스틱넷(ElasticNet)
   • 릿지(Ridge) 는 선형 회귀에 L2 규제를 추가한 회귀 모델입니다. 예측 영향력이 큰 피처의 회귀 계수 값의 크기를 줄여 다중 공선성을 제거합니다.
   • 라쏘(Lasso) 는 선형 회귀에 L1 규제를 추가한 회귀 모델입니다. 예측 영향력이 작은 피처의 회귀 계수를 0으로 만들어 예측 시 선택되지 않게 함으로써 다중 공선성을 제거합니다.
   • 엘라스틱넷(ElasticNet) 은 L2, L1 규제를 함께 결합한 모델로써, L1 규제로 피처의 개수를 줄이면서 L2 규제로 계수 값의 크기를 조정합니다.