개념

계층적 군집은 앞서 간단하게 소개했듯이 '응집형 군집'과 '분리형 군집'으로 구분할 수 있습니다. 사실 이 둘은 군집화 시작점과 진행 순서의 차이가 있을 뿐입니다. 계층적 군집화는 모든 개체들 간의 거리나 유사도가 미리 계산되어 있어야 하며, 한 번 분리된 혹은 병합된 군집은 다시 병합하거나 분리할 수 없다는 공통된 특성을 가집니다. (greedy algorithm)

계층적 군집화는 클러스터 개수를 미리 설정하지 않아도 되며 텍스트, 수치 상관없이 모든 클러스터링 기법에서 사용할 수 있다는 장점이 있습니다. 반면, 모든 쌍에 대해서 반복적으로 유사도를 구해야 하므로 계산량이 매우 많아 대용량 데이터에는 사용하기 어렵습니다.

계층적 군집화의 응집형, 분리형 기법에 대해서 각각 보다 자세히 알아보도록 하겠습니다.

1. 응집형

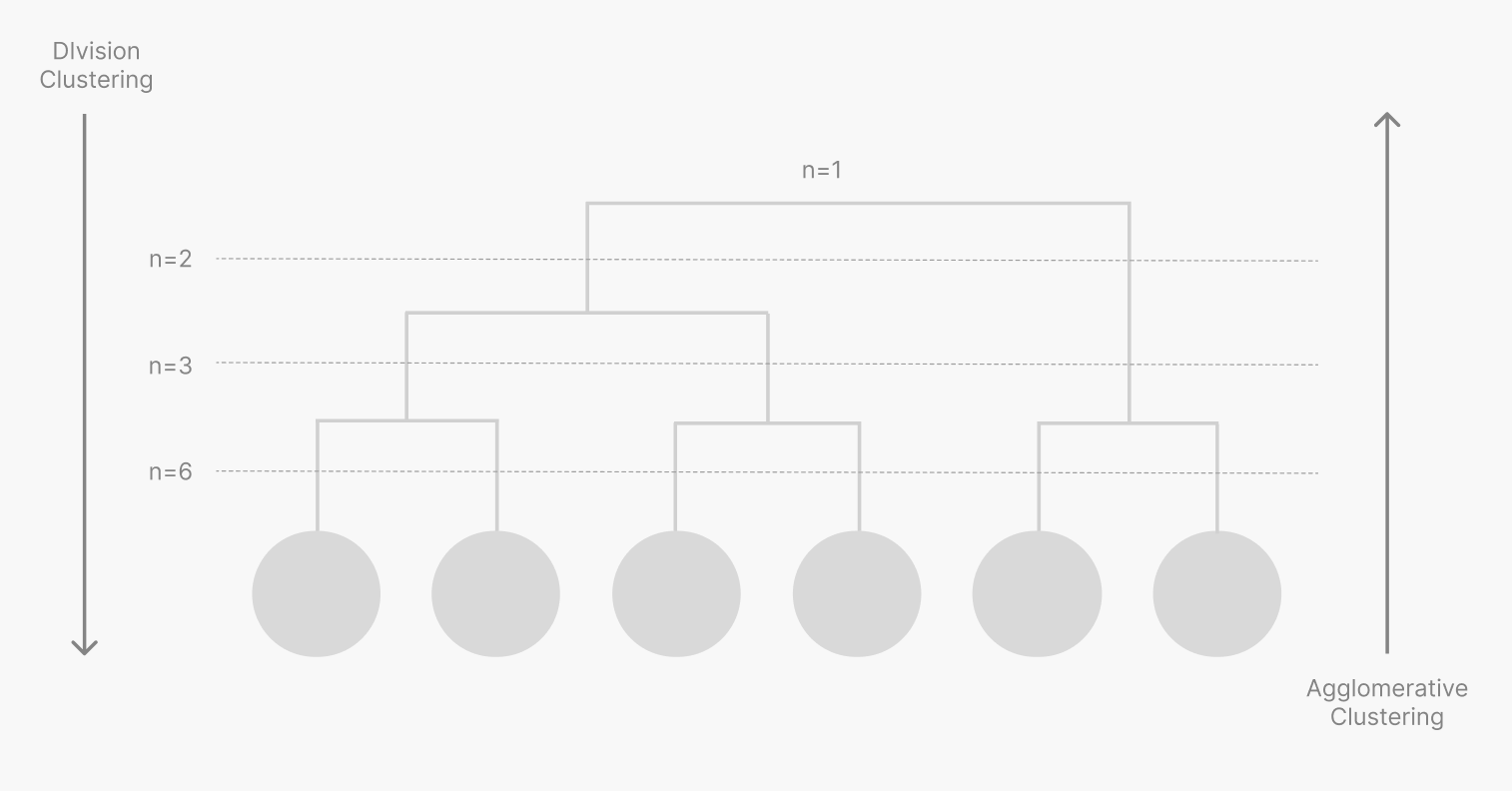
계층적 군집의 '응집형 군집 (Agglomerative clustering)'은 Bottom-up 방식이라고도 하며, 거리가 가까운 개체들을 합병하는 방법으로 군집화를 진행합니다. 응집형 군집은 반복적으로 두 개의 가까운 클러스터를 찾으며, 모든 데이터가 하나의 군집으로 묶일 때까지 반복합니다.

Dendrogram은 계층적 군집화를 시각적으로(Tree 모양) 나타낸 그래프로, 응집형 군집화에 많이 사용됩니다. Dendrogram으로 시각화한 그래프의 특정 부분을 잘라서 군집의 개수를 정할 수 있습니다. Python에서는 Scikit-learn을 통해서 간단하게 그릴 수 있으며, 공식 사이트의 문서를 참고해보세요.

✔️ Dendrogram의 원리

• 모든 개체들 간의 거리(혹은 유사도) 계산해서 행렬(matrix)을 만든다.
• 거리가 가장 가까운 개체 두 개를 묶어 하나의 군집으로 만든다.
• 위 에서 만든 군집을 포함하여 다시 거리 행렬을 계산하여 만든다.
• 이 과정을 모든 개체가 하나의 군집이 될 때 까지 반복한다.

참고자료: spicy.cluster.hierarchy.linkage, 계층적 군집화(Hierarchical Clustering)

이때 맨 처음 가장 가까운 두 개체를 하나의 군집으로 만들어주는 점은 모 응집 기법 두 동일하지만 이후 군집과 개체, 군집과 군집을 묶어주는 방식에 따라 다양한 응집 기법이 있습니다. 응집 기법의 종류는 다음과 같습니다.

1. 최단 연결법(Single Linkage Method): 가장 가까운 두 개체를 묶은 군집을 생성한 뒤, 가장 가까운 군집 두 개를 묶어 주는 방법입니다. 이상치들도 가장 가까운 개체와 묶일 수 있기 때문에 하기 때문에 이상치에 취약하다는 단점이 있습니다.
2. 최장 연결법()Complete Linkage Method): 가장 가까운 두 개체를 묶은 군집을 생성한 뒤, 가장 먼 군집 두 개를 묶어 주는 방법입니다. 최단연결법과 동일하게 이상치에 취약합니다.
3. 평균 연결법(Average Linkage Method): 가장 가까운 두 개체를 묶은 군집을 생성한 뒤, 각각 군집의 모든 개체들의 거리의 평균을 두 군집간의 거리로 두고 가장 가까운 군집 두 개를 묶어 주는 방법입니다.

최단, 최장 연결법과 동일하게 이상치에 취약하며 모든 거리의 평균을 계산해야 하므로 시간이 오래걸린다는 단점이 있습니다. 4. 중심 연결법(Centroid Linkage Method): 가장 가까운 두 개체를 묶은 군집을 생성한 뒤, 각 군집의 내부 중심과 다른 군집의 내부 중심 간 거리를 계산하여 가장 가까운 군집 두 개를 묶어주는 방법입니다. 평균 연결법과 동일하게 계산량이 많습니다.
5. Wards 연결법(Ward Linkage Method): 가장 가까운 두 개체를 묶은 군집을 생성한 뒤, 두 군집이 합쳐졌을 때 생기는 오차제곱의 합(SSE)이 최소가 되는 군집끼리 묶어주는 방법입니다. 두 개의 군집을 하나로 묶을 때 생기는 정보 손실을 최소화하는 방법으로 오차제곱합을 고려하기 때문에 이상치에 덜 취약하며 크기가 비슷한 크기의 군집끼리 병합되는 특성이 있습니다.

참고자료: 클러스터링(군집분석)-계층적 분석 , 클러스터링과 계층적 군집분석, 군집분석(clustering), 계산+코드 참고 자료

2. 분리형

계층적군집의 '분리형 군집 (division clustering)'은 Top-down 방식이라고도 하며, 거리가 먼 개체들을 분리하는 방법으로 군집화를 진행합니다. 모든 개체를 하나의 군집이라고 보고 시작하며 하나의 군집을 둘로 반복적으로 나눠가면서 진행합니다.

다이애나 기법(DIvisive ANAlysis) 은 유클리드 거리가 먼 순서대로 먼저 분리해가면서 최종적으로는 각각의 개체로 분리될 때까지 수행합니다. 다이애나 기법은 복잡도가 높아서 실제로 많이 사용되진 않는다고 합니다.

참고자료: Water | Free Full-Text | Low-Carbon Tour Route Algorithm of Urban Scenic Water Spots Based on an Improved DIANA Clustering Model (mdpi.com), 계보적방법(Hierarchical clustering)